Le
WAIS et le WAIS-R
Le WAIS s'adresse aux adultes.
En 1939, David Wechsler,
psychologue américain, publia une batterie de tests à
l'intention des adultes afin de mesurer leur intelligence. Wechsler
inventa un mode de calcul par tranche d'âge jusqu'à 59
ans permettant de transformer les scores obtenus en une seule note dont
la référence était fixée à 100 comme
pour le QI.
Le WAIS est l'échelle d'intelligence pour adultes de Wechsler
( avec celui de Stanford-Binet, l'un des types de tests les plus connus
). Il a été standardisé en 1954.
Quant au WAIS-R, il s'agit tout simplement de la version révisée
de ce dernier; sa standardisation date elle de 1978.
Le test est divisé en 2 groupes de subtests, permettant d'obtenir
une mesure de QI verbal (culturel) et de QI de performance (aculturel).
- Six épreuves verbales : information
et compréhension générales, raisonnement arithmétique,
mémoire immédiate, analogies, vocabulaire.
- Cinq épreuves de performance mettant en jeu les qualités
perceptives et les capacités d'analyse et de raisonnement du
sujet : classement et complètement d'images, assemblage de cubes
et d'objets, codification.
La
passation d'un tel test permettrait une analyse plus fine du type d'intelligence
de la personne évaluée.

--------------------------------------------------------------------------------
Le WISC
Le WISC est utilisé entre 6 ans et 16 ans et 9 mois.
( Le WPPSI-R
concerne les enfants de 2 ans et 11 mois à 7 ans et 3 mois )
Le WISC est l'échelle d'intelligence pour
enfants de Wechsler.
Il comporte
- 5 sous-tests verbaux : test d'information, de compréhension,
d'arithmétique, de vocabulaire, de similitudes,
- 5 sous-tests de performance, dans lesquels l'enfant doit copier des
dessins à l'aide de cubes à motifs, ordonner un ensemble
d'images, ...
Par exemple, il
est important dans le cas d'un enfant précoce de connaître
l'écart obtenu pour les parties verbale et performance du test.
C'est souvent l'occasion de constater ou d'expliquer les phénomènes
de dyssynchronie éventuels. Plus l'écart sera grand au
profit du verbal, plus le risque de problèmes de motricité
seront importants, par exemple.
Les résultats obtenus par l'enfant aux différents sous-tests
sont additionnés, et on calcule le QI en voyant où le
total obtenu se situe sur la courbe de distribution des scores WISC
pour l'âge correspondant. Cette courbe de distribution, essentielle
à la détermination du QI, correspond simplement au résultat
empirique obtenu lorsque le test a été standardisé.
Par convention, la moyenne obtenue par chaque tranche d'âge de
l'échantillon standardisé correspond à un score
au QI de 100. De nouveau par convention, la déviation
standard par rapport à cet échantillon équivaut
à 15 points de QI de différence. Pour un bon échantillonnage
et une distribution normale, cela signifie que les 2/3 environ de la
population d'une classe d'âge ont un QI compris entre 85 et 115.
Le QI reflète alors une position relative d'un individu par rapport
à sa classe d'âge, et non un résultat isolé.
Dans le WISC, le score moyen d'un enfant de 9 ans est plus élevé
que celui d'un enfant de 6 ans en valeur absolue, mais ils ont tous
deux un QI de 100 car ils se situent au milieu de la
courbe de distribution. D'une certaine manière, en valeur
absolue, un enfant normal devient de plus en plus intelligent en grandissant.
Mais on peut dire aussi que son intelligence reste relativement
stable : bien que les scores pris en valeur absolue ne cessent d'augmenter
durant les années d'école, le QI d'un individu change
rarement au-delà de l'âge de 5 ou 6 ans.

--------------------------------------------------------------------------------
Le test de Stanford Binet
Le premier véritable test de QI moderne a été
mis au point par Alfred Binet(1857-1911) en 1905.
Il était mandaté par le ministère français
de l'Education pour élaborer un test permettant de repérer
objectivement et précocement les enfants ayant peu de capacités
scolaires, afin de pouvoir les envoyer dans des écoles spécialisées.
(argh!)
Le test Binet, ou test
Binet Simon, avait déjà quasiment toutes les caractéristiques
des tests actuels. Ses questions ont été posées
à un très grand nombre d'enfants. À chaque question
correspond un "âge intellectuel", qui est l'âge
auquel la moitié des enfants au moins est capable de répondre
à la question. Si une réponse ne permettait pas d'établir
une corrélation avec l'âge, elle était automatiquement
supprimée. Les questions pertinentes ont ensuite été
classées de façon croissante, en fonction de la maturité
intellectuelle à laquelle elles correspondaient, et ont été
posées dans ce même ordre aux enfants. Enfin, selon les
questions sur lesquelles l'enfant bloque, il est possible d'évaluer
sa maturité intellectuelle.
Le Stanford Binet
En 1916, Lewis Terman, un psychologue de l'université américaine
de Stanford établi un nouveau test d'intelligence inspiré
des travaux de Binet et Stern, le Stanford-Binet.
Terman introduisit alors la notion de "quotient intellectuel"
qui donna naissance au test de QI tel qu'on le connait aujourd'hui.
Il propose une échelle de calcul couvrant les différentes
facettes de l'intelligence.
Le test Binet a été traduit en différentes
langues et a été couramment utilisé dans les années
70 sous le nom de test de Stanford-Binet.
--------------------------------------------------------------------------------
Définitions
plus détaillées (calculs et stats) sur le site Expressions
généralistes

--------------------------------------------------------------------------------
Le test de Cattell
Le psychologue américain McKeen Cattell fut le
premier à employer le mot de "test" pour désigner
une série d'épreuves destinées à évaluer
l'intelligence de ses étudiants. Elève du célèbre
Sir Francis Galton, pionnier de la recherche sur l'intelligence
humaine au XIXe siècle, McKeen Cattell avait élaboré
des expériences permettant de mesurer la perception globale d'un
sujet : vision des couleurs, sensibilité auditive et visuelle,
perception de la douleur, etc. De nos jours, on rencontre encore différents
tests mis au point par Cattell comme le 16PF que les recruteurs affectionnent
particulièrement pour mesurer l'anxiété, l'extraversion,
la sensibilité et l'indépendance des candidats à
l'embauche.
Notons que son écart-type est de 24, et non de 15 comme le WISC.
Donc, les deux notes obtenues par un même individu, en dehors
du fait que ce sont deux tests différents, varieront forcément,
115 au WISC correspondant à 124 au Cattell.

--------------------------------------------------------------------------------
Le K.ABC
Le K.ABC (Kaufman & Kaufman, 1983 version
américaine, 1993 version française) s'adresse aux enfants
âgés de 2 ans 1/2 à 12 ans 1/2. Ce test a pour but
de mesurer l’intelligence et les connaissances, son originalité
est qu'il mettrait plus l’accent sur le processus que sur le contenu.
Il comporte deux échelles d’intelligence
distinctes.
- "L’Échelle des Processus Séquentiels"
mesure la capacité d’un enfant à résoudre
des problèmes en traitant mentalement les stimuli selon un ordre
sériel, par exemple dans la reproduction d’une
série de données de mouvements de mains effectuée
par le psychologue.
- "L’Échelle de Processus Simultanés"
mesure la capacité à résoudre des problèmes
nécessitant l’organisation et l’intégration
de nombreux stimuli de manière parallèle ou simultanée
comme identifier un dessin (fait de “taches d’encre”)
incomplet, résoudre des analogies visuelles abstraites.
La troisième échelle d’intelligence globale
est "l’Échelle des Processus Mentaux Composites",
combinaison des Échelles "Séquentielle" et "Simultanée".
Le K.ABC s’appuie comme le mentionne A. Kaufman,
le moins possible sur le langage, les informations et les compétences
acquises. Ces échelles font appel à la notion d’intelligence
fluide définie par Cattell et Horn (Horn et Cattell,1966)
c’est-à-dire comme un fonctionnement souple et adaptable
face à des problèmes liés à des situations
nouvelles.
Un avantage du K.ABC est de tester des enfants présentant
des handicaps auditifs, des troubles de la parole ou du langage ou non
francophones, les tâches qui le composent pouvant être indiquées
par gestes et les réponses se situer uniquement dans le registre
moteur. Par contre, les enfants handicapés visuels sont pénalisés
au K. ABC à cause de l’importance des stimuli visuels.
Extraits de K.ABC.
Pratique et fondements théoriques, de
A.S. Kaufman
Plus sur le K.ABC

|
|
Le Quotient Mental de Stern, ou Quotient
Intellectuel
Le psychologue allemand Wilhelm Stern, lecteur des travaux
de Binet, transforma la notion de niveau mental
en celle d'âge mental. En 1912, Stern détermina une forme
facilement compréhensible du calcul de l'intelligence,
qu'il désigna sous le terme de "quotient mental". Son
équation était la suivante : le quotient mental est l'âge
mental divisé par l'âge réel multiplié par
100. Un enfant de 8 ans ayant un âge mental de 10 ans aura donc
un QI de 10/8 x 100 = 125.

--------------------------------------------------------------------------------
La Courbe en cloche
Si les résultats des tests de QI donnent des courbes en cloche,
dites "Courbes de Gauss", c'est tout simplement parce qu'ils
sont... étalonnés pour le faire : ils comportent un petit
nombre de questions très difficiles (à laquelles très
peu répondront), un petit nombre de questions très simples
(seules les personnes ayant un retard intellectuel n'y répondront
pas) et le gros des autres sert à évaluer ceux qui sont
dans la moyenne. Les questions sont donc ajustées et étalonnées
jusqu'à ce que leurs résultats produisent la fameuse courbe
en cloche. La grande majorité doit répondre
aux 3/4 des questions, par exemple, et une minorité ne répondra
qu'à 1/4 seulement, une autre minorité répondant
à presque toutes !
La loi de Gauss ne s'y applique ni plus ni moins
qu'à toute information bruitée.

Exemple de courbe en cloche : la répartition du QI dans la
population
Loi de Gauss : La
répartition d'une population "normale" peut être
représentée selon une courbe en cloche.
Dans une population donnée (les reçus au Bac, des billes
dans un sac, etc.), si on classe les individus selon une caractéristique
(leur taille, leur poids, leur QI, leur niveau de compétence),
on s'aperçoit que, plus on s'approche de la moyenne sur le
critère considéré, et plus il y a d'individus.
Plus on s'en éloigne, et moins il y en a. Aux deux extrémités,
il n'y a presque personne. La représentation graphique de cette
réalité s'appelle une Courbe de Gauss et prend
la forme d'une cloche.
> Application commerciale : La courbe
de Gauss est bien pratique pour représenter la réalité
d'un marché. Les clientes adultes qui mesurent 150 cm et celles
qui mesurent 200 cm vont, par exemple, se retrouver placées
en dehors de la cloche, à chacune des extrémités
de la courbe. Faut-il pour autant se désintéresser de
leur sort au prétexte qu'elles sont peu nombreuses ?
La
Loi "normale" de Gauss sur Wikipedia.org,
l'encyclopédie libre

--------------------------------------------------------------------------------
L'écart-type
ou déviation standard, et la variance
Plus communément appelée
ECART-TYPE, la déviation standard caractérise
la largeur de la distribution. Elle est exprimée mathématiquement
comme étant la racine carrée de la variance,
celle-ci mesurant la distribution des valeurs autour du centre de
la courbe.
Écart-type (S) = Racine carrée de la variance
L'écart-type est la mesure de dispersion,
ou étalement, la plus couramment utilisée en statistique
lorsqu'on emploie la moyenne pour calculer une tendance centrale.
Il mesure donc la dispersion autour de la moyenne. En raison de ses
liens étroits avec la moyenne, l'écart-type peut être
grandement influencé si cette dernière donne une mauvaise
mesure de tendance centrale.
Contrairement à l'étendue et aux quartiles, la variance
permet de combiner toutes les valeurs à l'intérieur
d'un ensemble de données afin d'obtenir la mesure de dispersion.
La variance (symbolisée par S2) et l'écart-type (la
racine carré de la variance, symbolisée par S) sont
les mesures de dispersion les plus couramment utilisées.
La variance est définie comme étant la moyenne
arithmétique des carrés des différences entre
les valeurs observées et la moyenne. C'est une mesure du degré
de dispersion d'un ensemble de données. On la calcule sous
la forme de l'écart au carré moyen de chaque nombre
par rapport à la moyenne d'un ensemble de données.
Par exemple : Si par convention, la déviation
standard par rapport à un échantillon équivaut
à 15 points de QI de différence, cela signifie que les
2/3 environ de la population d'une classe d'âge ont un QI compris
entre 85 et 115 --> Voir la Courbe de Gauss
;-)
Généralement, plus les
valeurs sont largement distribuées, plus l'écart-type
est élevé. Imaginez, par exemple, que nous devons
séparer deux ensembles différents de résultats
d'examens de 30 élèves; les notes du premier examen
varient de 31 % à 98 % et celles du second, de 82 % à
93 %. Compte tenu de ces étendues, l'écart-type serait
plus grand pour les résultats du premier examen.
Il n'est pas toujours facile d'évaluer
l'importance que doit avoir l'écart-type pour que les données
soient largement dispersées.
L'importance de la valeur moyenne de l'ensemble des données
dépend aussi de l'importance de l'écart-type. Lorsque
vous mesurez quelque chose en millions, le fait d'avoir des mesures
qui se rapprochent de la valeur moyenne n'a pas la même signification
que si vous mesurez le poids de deux personnes.
Par exemple, si après avoir mesuré les
recettes annuelles de deux grandes entreprises, vous constatez un
écart de 100 000 euros, la différence est considérée
comme étant peu significative, alors que si vous mesurez le
poids de deux personnes, dont l'écart est de 30 kilogrammes,
la différence est considérée comme étant
très significative.
Voilà pourquoi il est utile, dans
la plupart des cas, d'évaluer quelle est l'importance de l'écart-type
par rapport à la moyenne de l'ensemble de données.
Voir l'article "Variance
et écart-type" sur le site Statistiques
Canada (réservé aux matheux !) et son glossaire
pour les termes utilisés.

--------------------------------------------------------------------------------
L'effet Flynn
Accroissement lent et inexorable
du rendement moyen à des tests de type Q.I. que l’on
observe depuis 100 ans dans les pays industrialisés.
Selon le professeur James R. Flynn, dans les pays où on a
pris l’habitude d’utiliser ces tests, le QI a progressé
en moyenne de trois points par décennie. Et les gains apparaissent
là où on s’y attendrait le moins : dans les
tests qui minimisent l’apport culturel. L’écart
de rendement cité plus haut a été en effet
démontré avec l’outil que d’aucuns considèrent
comme étant le moins “chargé” culturellement
: les matrices progressives de Raven ! (voir en page de tests un
test qui s'en approche)
Ce sont les tests les plus liés aux matières
scolaires qui connaissent les plus faibles progressions.
MAIS, paradoxalement, l'accroissement de la scolarité, et
le niveau scolaire, est un facteur qui joue dans l'augmentation
des scores aux tests aculturels !
Les causes ?
On pense à l'augmentation de la qualité de la nutrition,
l'allongement et la généralisation de la scolarité,
et au fait que les parents accordent plus précocément
de l'attention à leur enfant.
Philippe Dumas défend l'idée que l'exposition intensive
des tout jeunes aux objets des Tic (Technologie de
l'Information et de la Communication) est un des facteurs-clé
de l'effet Flynn (l'augmentation générale du QI et
de la demande de stimulation intellectuelle), alors que pour Francis
Heylighen : "Un
facteur plus général est que cette société
dans l'ensemble fonctionne à un niveau intellectuel plus
élevé, proposant à l'enfant curieux plus d'informations,
de défis plus intellectuels, de problèmes plus complexes,
plus d'exemples à suivre, et plus de méthodes de raisonnement
à appliquer. Juste en utilisant les appareils quotidiens,
tels que les fours à micro-ondes, et les thermostats, exige
un type plus abstrait de raisonnement dont la génération
plus ancienne est souvent incapable. La plus grande complexité
de la vie est susceptible de stimuler une plus grande complexité
d'esprit. L'utilisation croissante des ordinateurs pour l'éducation
ou les jeux précoces est susceptible d'augmenter la connaissance
générale, le raisonnement abstrait et l'agilité
intellectuelle".
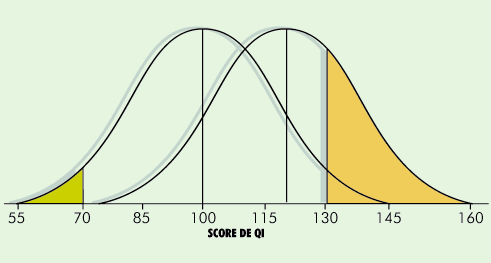
Si on gardait le même étalonnage, les
mêmes enfants, surefficients il y a 100 ans, seraient dans
la moyenne de nos jours (écart de 30 points).
Il faut donc réactualiser régulièrement
les tests. On le fait en moyenne tous les dix ans, en ré-étalonnant.
Une personne passant donc les deux versions d'un même test
aura par exemple 105 à l'ancienne version et 102 à
la nouvelle.
On a cru longtemps que les capacités
intellectuelles baissaient avec l'âge... La prise en compte
de l'effet Flynn fait prendre conscience que nos capacités
baissent sans doute bien moins qu'on le croyait de prime abord.
C'est plus alors notre capacité d'adaptation (d'ajustement
à la nouvelle génération ?) et l'écart
avec les performances des jeunes qui serait en cause !
(Vieux surefficients, réjouissez-vous
--> vous savez parler aux jeunes !!)
Sources :
John Horgan, in Get Smart, Take a Test, Scientific American,
Novembre, p.12-13 - 1995
Francis Heylighen, Increasing
intelligence : the Flynn effect en anglais site recommandé
par Michel
Duguay (Université canadienne)
Philippe Dumas, Nouveaux
dispositifs pédagogiques et crises des systèmes éducatifs.
Nhan, Vous
avez dit QI ?, étudiant à l'UFR De UFR
de mathématiques et Informatiques René Descartes.
|



